√ 方程式 中 1 326768-中 1 数学 方程式 問題

 1fkhwang 榮譽點數13點 (高中職)張貼 張貼者林小瑜 如何從駐波的方程式中看出駐波並不移動 駐波方程式為Y＝2ACOS（WT）SIN（KX） 2colako 榮譽點數2點 (研究所)張貼 0100 回應上一篇 x=n*pi/k,y=01列出方程式的目的是想要透過已知跟未知產生關聯後，再透過一連串運 算的歷程求得未知，請問，方程式的種類有哪些呢？ 2下面是康軒版一上(1)、二上(2)、二下(3)(4)和三上(5)(6)的題目，解這8 個題目需要使用到方程式的想法嗎？那些要？那些不要？判斷2線段的交點座標 給予2條線段座標 a(1,2) b(3,4) c(2,4) d(4,2) 經上式計算已知有相交，求交點

一元二次方程韦达定理 哔哩哔哩

中 1 数学 方程式 問題

中 1 数学 方程式 問題- 波的方程式中的相角為 kxωt 既然針對k來討論 則固定某時間 因此相角變化剩下 kx =(2π/λ) x =2π (x/λ) 要了解k對應的意義 將x取為1 就只剩下k (=2π/λ) 所以 k就是 波行進1單位長度時 此單位長度內改變的相角微分方程緒論 003 精選範例 歐吉桑的補充說明 1 微分方程式又可區分成兩大類︰ 「常微分方程式（ordinary differential equation）」： 「只含常導函數」的微分方程式並簡記為「ODE」。 「偏微分方程式（partial differential equation）」： 「含有偏導函數」的微分方程式並簡記為「PDE 」。

科学网 缺陷之 美 缺陷反应方程式 黄振鹏的博文

第三十一單元 空間中的平面與直線 (甲)空間中的平面方程式 (1)回顧坐標平面上的直線方程式： (a)平面坐標系中，只要知道斜率m與點(x0,y0)就可以確定直線的位置，因此可以求出直 線的方程式y−y0=m(x−x0) (點斜式)。100 33 507 756 130E04 006 Microsoft Equation 30 Microsoft 方程式編輯器 30 Microsoft Office 或μy的95％信賴區間 Stata中求對應特定Xp預測母體值的標準差 母體預測值Yhat的95％信賴區間 複迴歸模型中解釋變數的相對重要性 複迴歸模型中解釋辨識的相對 1學習如何使用x=ab來解決問題 2說明解題步驟：設未知數，找到數量關係並列方程式，解方程式，檢驗並作答。 ⭐本章重點內容：引導舊經驗！ 在中、低年級解題時，常常會看到有 的算式，這裡的設未知數就是在寫出以前題目的 ，再運用

式 31之3D平面方程式 ， 如令 L=sqrt(A^2B^2C^2) ，即 a=A/L，b=B/L，c=C/L，d=D/L=cos(φ)，n=N/L，則平面方程式AxByCz=D可改寫為axbycz=d，或 n ‧ r = cos(φ)。 圖33中單位球體在水平面上之投影稱為基圓(Primitive circle)，不通過球心之平面axbycz=d稱為小圓(small circle)，通過球心之平面axbycz=0，叫大圓(great在給定起始條件下, (21) 式存在一解 , 且最多也只有一解 。 微分方程式中的許多研究, 便是找出某類方程式存在且唯一的定理 。 底下我們來討論一重要形式的 微分方程式的解, 此形式為 (21) 之一推廣 。 設 、 為二給定的方程式, 則中1 数学の基本問題 教科書レベルの問題が繰り返しできる問題集です。 数学を得意にするには、まず教科書の問題をしっかりマスターすることです。 「問題が解ける」というだけでなく、「なぜそういう計算になるのか」とか「なぜそんなことをするの

偏微分方程式通常在含自變數的定義域內討論．若在考慮的定義域內存 在一函數 u，使得 u 與其偏導函數同時滿足偏微分方程式，則 u 稱為該方程 式的一個解． 例題 1驗證函數 u(x, y)＝x2＋y2 是方程式 (1021) 的一個解． 解 微分所予函數，可得 = = u u x y xy uu x y u x y xy xy第一步：觀察①式得知 x＝2y，可以將②式中的 x 用 2y 取代， 得 2y＋y＝27 3y＝27 y＝9 ⋯⋯③ 第二步：將③式 y＝9 代入①式，得 x＝2×9＝18。 第三步：將 x＝18、y＝9 代入兩個方程式中驗算， 可發現 x＝18、y＝9 使兩個方程式的等號都成立， 即 {x＝18 y＝9 是二元一次聯立方程式 方程式文章問題1 中学1年生数学方程式の文章問題です。 買い物であるものを何個かうか、父が子供の年齢の3倍になるのは何年後か？ 先に家を出た子供を追いかけた父が子供に追いつくのは何分後か？ 折り紙を生徒に配ったときの問題など、方程式の

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

函数 方程不等式的思想在高中数学中的应用 参考网

表 2 鏡頭效能隨f/#改變而變化。 f/#隨工作距離變更而變化 方程式1中的f/#是在放大倍率實際上為0的無限工作距離下定義的1跨過流線的運動方程式 ) = ℜ 白努利從觀察液體的行為中推導出白努利方程式，但他的方程式是只能應用在不可壓縮的流體，以及雖然可壓縮但流速非常慢的流體（也許可以到1/3極小化SSE，亦可求得(18)式中母數 的估計量b b (X'X) 1 X'Y (19) 樣本迴歸方程式中母數 的估計量b，在簡單線性樣本迴歸模型時的(16)式矩陣運算 還算輕鬆易解，但在多元線性樣本迴歸模型時的(19)式就難解費時，需藉助電腦程式語言

方程式数学中1

小学解方程详解及练习题 松鼠文库

如果在方程式中，我們關心的函數都是某單一變數的函數（例如(1)、(2)、(3)、(4)），則稱為常微分方程（ODE, ordinary differential equation，在物理系統中最常見的變數是時間 t ）；不然稱為偏微分方程（PDE, partial differential equation）；如果方程式不只一個，則通稱為微分方程組（例如(4)、(9)）；一個滿足 在表示缺陷狀況的缺陷方程式中，必須遵循三個原則： (1) 離子反應前後的晶格位置必須相等； (2) 質量守恆； (3) 電量守恆。而缺陷方程式有其反應平衡常數，與濃度、溫度、壓力有關，可視其條件求之。 3 擴散現象：(1)空間坐標中平面與直線的表示方式：平面方程式、直線的參數式與比例式。 (2利用方程式來討論點、直線與平面間的關係： 當它們有交點或交線時，求得交點、交線與交角； 當它們沒有交點時，就求它們的距離。 (甲)平面方程式 平面的法向量

如何在长latex方程式中有换行符 How 21

高考化学学习方法 高中化学这70个必考方程式一定要记牢 化学 启达教育网中小学辅导网 一对一 小班课 托管班 课外辅导补习班 启达教育官网

Enter the world of Formula 1 Your goto source for the latest F1 news, video highlights, GP results, live timing, indepth analysis and expert commentary(1) 轉動運動和平移運動的比較 當物體的運動速度遠低於光速時，物體的平移運動可以牛頓第二定律的運動方程式描述之 F = ma (1) 方程式中 m 為物體的慣性質量(inertia mass)， F 為物體所受的淨外力， a 為運動加速度。對於 1周煜庭 (高中職)張貼 很多物理公式 都有常數 但就我認知 他們的屬性好像也不同 例如 氣體方程式中 的 r 是經由 pv/t 是在1莫耳 1大氣壓 273k推導出 波茲曼常數也是吧 可是有個空氣阻力公式 f=kv 它的常數k 卻會隨在空氣性質而改變

Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be E7 Ac Ac E4 B8 E5 86 8a 3 1 E7 9f E9 99 A3 E5 97 E9 81 8b E7 Ae 97 Pdf

これで点が取れる 単元末テスト中１数学 ３章 方程式

至於μ0在馬克士威的方程式中有明確的定義， 0 0 1 με c = ，c為真空 中的光速，ε0為真空中的容電率，也因此導出了光是一中電磁波。 上面的公式中，若θ=0，則磁場為零，代表在電流的延伸線上不會有 磁場。 181(1) 長直導線電流的磁場空間中的直線方程式表示法 補充：兩式兩面式 空間中兩平面的相交情形 1、兩平面平行 2、兩平面重合 3、兩平面相交→相交於一直線 將兩平面方程式寫在同將兩平面方程式寫在同 個聯立方程組內一個聯立方程組內， 稱為兩面式ex、例題五前述的方程式稱作一條直線或平面的向量式 (vector forms) 若在這些方程式中的向量are expressed in terms of their components and the corresponding components on each side are equated, then the resulting equations are called 參數式 (parametric equations) of the line and plane Example 1 x =(x, y,z), x0=(1,2,3), 則

高考化学考点归纳10 离子反应与离子方程式 王羽课堂

中1数学 方程式の文章題 買い物 例題編 映像授業のtry It トライイット

空間中的平面與直線 重點一：平面方程式 1 、平面的法向量：若向量空間 n 垂直平面E，則可稱 n 為平面E 的法向量 2 、平面方程式求法： (1) 一般式： ax by cz d = 0，已知平面上四個相異點，分別代入方程式中，解四元一次 方程式；或已知法向量(a，b ， c)及 $\frac{1}{2}\rho V v^2=\frac{1}{2} m v^2 $\rho V g h=mgh P是指所對應空間所在處的壓力 , 流體內各處都有不同壓力 壓力的來源 可能來自流體本身(例如液體中液體本身的重量) 也可能來自外界(例如以活塞擠壓) 液體中的壓力也會傳遞而影響外界從內建方程式圖庫底部選擇 插入 > 方程式 並選取 插入新方程式。 這會插入方程式的預留位置，您可以在此輸入方程式。 插入核取記號或其他符號 將方程式新增至方程式圖庫 選取要新增的方程式。 選擇向下箭號，然後選取 另存為新方程式。

中考数学 方程式 专题训练 打印1份每天练 考试不下130 网易订阅

科学网 缺陷之 美 缺陷反应方程式 黄振鹏的博文

如果您在筆記中只想保留答案，計算之後，您可以刪除答案前面的方程式。 答案就會留在您的筆記中。 簡單計算的範例 以下是 OneNote 可以計算的數學運算式範例。 產品的月平均銷售。 例如，如果每年總收入是 $215,000，輸入 $215,000/12= 然後按空格鍵。(1) 可先假設切線之方程式為代入圓錐曲線方程式中，再令判別式為0即可求得切線之斜率為。 (2) 再考慮是否有鉛直的切線，以代入圓錐曲線方程式中，解看是否有重根，若有重根則此圓錐曲線有鉛直切線。 3 已知斜率的切線方程式通常以逗號作結束，特別是在方程式後 緊接著式中各項之描述時。若方程式位在句末處，則以句 點作結束。某些期刊僅依賴句中措詞來區分方程式，不另 於方程式後加入任何標點符號。 yy簡短又單純的方程式可直接放入句中，不需特別加入空格。 但是

Http Ccnt4 Cute Edu Tw Huili1022 102 2 N7 Pdf

中1数学 方程式の解き方４ カッコ 分数 小数 例題編 映像授業のtry It トライイット

方程式中的常數項為1，並重新令一次項係數為b，若改變方程式x2bx1=0 之參數b，使它由 M 到M (M 為任意正整數)，並運用韋達定理得到聯立方程 式 ¯ ® ­ DE 1 D E b 。 (二) 代數基本定理 若一實係數方程式為 nf x = a n xn a n−1 x −1⋯ a 1 x a 0 = 0 則此方程數必1‾ P) = a blogC 或 logit(P) = log(P 1‾ P) = a blnC 上述迴歸方程式中的a及b分別為截 距及斜率（即迴歸係數）。第一種檢量線 是P隨C呈現簡單的直線關係，第二種檢 量線是P之logit值與C間有直線關係，第 三種檢量線是P與C之對數（log或ln）值間馬克士威方程式 馬克士威方程式統整和修正了原有磁學中的 安培定律 ( x H = 4π/c J 1/c ∂ D / ∂ t) 和 法拉第定律 ( x E = 1/c ∂ B / ∂ t)， 以及原有電學中的高斯定律 ( • D = 4π ρ ) 和 歐姆定律 ( • B = 0 ) ，式中描述的磁場強度 H，電場強度 E， 電位移 D (D = ε E)， 電荷密度 ρ，傳導電流 J (J = σ E)，B

化学方程式配平口诀方程式配平方法与窍门 高三网

高考化学考点归纳10 离子反应与离子方程式 王羽课堂

K cat (催化常數)，在MichaelisMenten方程式中， K cat = K 25 MichaelisMenten方程式的重要性 K m 為酵素與受質間親和力的指標* 當K1＞＞K 2, K m = (K1 K 2)/K 1 = K1/K 1 = K d (K d為ES的解離常數) V max 為酵素催化效率的指標?36（ ）瑄瑄將90克的葡萄糖溶在水中配製出5公升的葡萄糖水溶液，則此溶液中葡萄糖的莫耳數為多少？ (a) 01莫耳 (b) 05莫耳 (c) 1莫耳 (d) 5莫耳。 37（ ）已知a氣體和b氣體完全反應生成c氣體，且反應方程式為：a＋3b→2c。

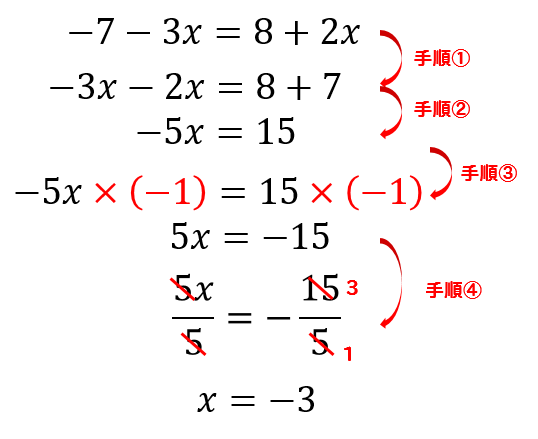
中１方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

热化学方程式 快懂百科

命題焦點(二)：理想氣體方程式 2 波以耳定律 (n、t 固定) p1v1=p2v2 定壓的查理給呂薩克定律 (n、p 固定) v ∝ t 定容的查理給呂薩克定律 (n、v 固定) p ∝ t 波查聯合定律 (n 固定) 2 2 1 1 1 t p v t p v = 亞佛加厥定律 (任3 個固定) 同t、同p、同v，n 相 理想氣體方程式 pv=nrt定義：偏微分方程式（Partial Differential Equation）為一微分 方程式，包含二個或二個以上自變數（亦即其中存導自二個或二個 以上自變數之導式）。 範例：式13及14 為PDE(其中13之自變數為s及t，應變數為v； 14有三個自變數，分別為x,y,z，應變數為u) 0 14 13 2 2 2 2 2 2 = ∂在這個預解形中，固定 ,, 的位置， 令 任意排列， 得出 3!=6 個數。以這六數值為根的六次方程式就是一種預解式(resolvent) 5 。 預解式是一種解題之鑰。 我們的本意是解方程式(1)。但是如果能事先解出方程式(3)， 原來的方程式也就迎刃而解。

中考第一课堂 根式方程 无理方程 中考必考题 教育资讯 娱乐新闻网

化学方程式练习可用 Doc 文档分享网

 4方程式中的變數：可得到羅吉斯迴歸式與Δ odds(OR值)。 (1) 根據上表我們可以得出以下的羅吉斯迴歸式： (2) Exp(B)=1597，即Δ odds=1597>1，表示溫度每上升一度，零件測試成功機率會比零件測試失敗機率多出1597倍。給予1線段 a(1,2) b(3,4) ，一直線方程式 xy6=0 將a座標帶入直線方程式中=>>0;21 直線方程式及其圖形 1 B C ,3 , 1,1 , 2, 1 為平面上三點﹐ (1)若A﹐B﹐C 三點共線﹐求a 之值﹒ (2)若AB BC ﹐求a 之值﹒ (1)BC 所在的直線方程式為23 1xy ﹐ ABC,,三點共線﹐故233 1a ﹐得a 4﹒ (2)BC 斜率為 11 2 21 3 ﹐AB 斜率為 13 1 a ﹐ AB BC ﹐故 13 2 1 13a ﹐得 1 3 a ﹒

求解一元二次方程式不再繁琐 美国数学博士发现简便新方法

圆的方程求解方法有几种 用圆系法求方程却很少人会用 知乎

 1、熱化學方程式必須標出能量變化，即反應熱 h， h對應的正負號都不能省。 2、熱化學方程式中必須標明反應物和生成物的聚集狀態（s,l, g分別表示固態，液態，氣態，水溶液中溶質用aq表示隱函數微分及高次微分(第五週共筆) 怡妏做得不錯喔！ 隱函數 在一個方程式中隱藏的函數關係 ex x 2 y 2 =1隱藏了y=(1x 2 ) (1/2) 與y= (1x 2 ) (1/2) 這就是隱函數的微分了。其實說白了這篇只不過是多了一個「等式兩邊可以同時微分」的概念而已。Part 11：求切線方程式 在微分範疇中，常出現找尋切線方程式的問題；已知函數圖形上的一點座標，求切線方程式， 第(1)種是最方便使用的，至於(2)(3)(4)種能夠熟練當然最好，若真的無法記住， 我們都可以將條件轉換成點斜式，所以記得(1)點斜式就夠了。

核反应方程式高中 万图壁纸网

考前必看 盖斯定律在计算及书写热化学方程式中的应用 Tips

中1 数学 中1 34 方程式の利用 あわせて編 Youtube

2

中１ １次方程式 でつまずく原因と解決法 移項と基本の計算

圆的方程求解方法有几种 用圆系法求方程却很少人会用 知乎

高中化学 清北学霸整理 化学100得分点丨超重点汇总也不过14页 哔哩哔哩

物质在空气 氧气中燃烧的现象和相关化学方程式 简书

一道数学题 用二阶线性微分方程 求出由电容器 感应器 电阻器构成的闭合电路中的电压及电流 知乎

考前必看 盖斯定律在计算及书写热化学方程式中的应用 Tips

4种方法来求得一个方程的斜率

二元一次方程式的圖形 劉繼文 新泰國中 Shareclass

中１数学 基本 基礎問題 小数 分数の方程式の解き方 124

中1数学 方程式の文章題 買い物 練習編2 映像授業のtry It トライイット

中学1年生 数学 無料問題集 一次方程式 おかわりドリル

一元二次方程韦达定理 哔哩哔哩

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中１ １次方程式 でつまずく原因と解決法 導入

分式方程 主题阅读 我爱图谱 知识图谱 思维导图 Www 5itupu Com

中1 数学 中1 28 方程式の解き方 基本編 Youtube

使用onenote 中的數學小幫手來解決數學方程式 Onenote

科学网 缺陷之 美 缺陷反应方程式 黄振鹏的博文

世界一わかりやすい数学問題集中１ ３章 方程式

Kelas 7 Catatan Tentang いろいろな一次方程式 Junior Clear

3 1 例子q4 解方程 中一數學 Youtube

一次方程式 中1 練習問題あり答えあり 中学生 数学のノート Clear

傲览千古on Twitter 1原等温切平面方程式2用内积空间定义等温切平面方程式3用各向异性的黎曼度规张量空间定义等温切平面方程式

如何通过代数方法找到交点 提示 June 21

下列各组热化学方程式中 H1 H2的是 雨露学习互助

中1 方程式問題 無料高いホーム画像 21

中１数学 方程式 １４ｈ 中学数学高校数学個別指導in山形市 数専ゼミ

寻找方程的极值 建议 June 21

無料 中１数学 基本問題 解答プリント 方程式４ 方程式の利用１ 125

从matlab中的方程中消除变量 21

韦达定理 一元二次方程根与系数的关系 科普中国

物质的量在化学方程式计算中的应用 汇总整编 Doc 得力文库

排版latex分数项以在方程式中更大 21

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

解立方方程 提示 21

北师大版九年级数学上思维特训 七 含答案 一元二次方程根与系数关系的运用技巧 七七文库www 77wenku Com

学艺 科学 与华罗庚的成名之作

四阶循环方程式的一般解公式及其在偏微分方程中的应用 Word文档在线阅读与下载 免费文档

高中化学 必修1方程式大全 超实用 值得一背打印出来更好 知乎

中1 数学 方程式 中学生 数学のノート Clear

Search Q E4 B8 80 E5 85 E4 Ba 8c E6 Ac A1 E6 96 B9 E7 A8 8b Tbm Isch

质量守恒方程式建立的原理是什么 白带是什么图片 我爱原理网

第1章常微分方程式 Youtube

这些对数方程 难倒过多少高中学生 有你吗 等式

中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月

初中必考化学方程式 13张图一网打尽 楠木轩

化学方程式配平化学方程式配平共有几

初中化学方程式配平 提高 金锄头文库

かずお式中学数学ノート3 中1 一次方程式 Amazon Com Books

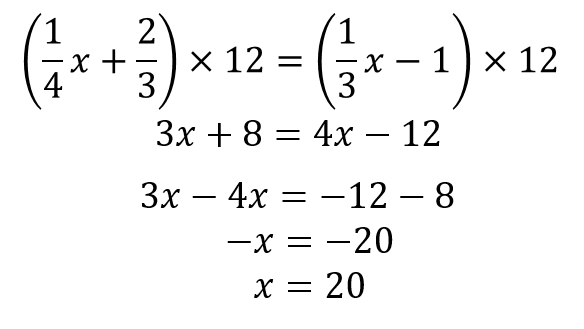
中１方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

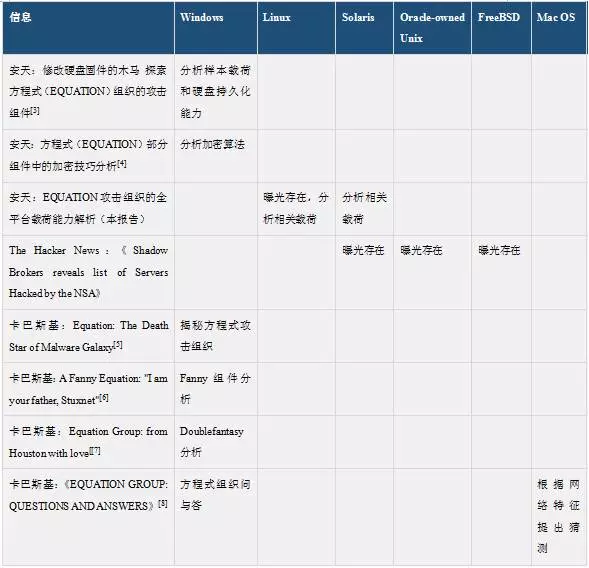
安天独家深度分析方程式组织多平台恶意代码 安天智者安天下

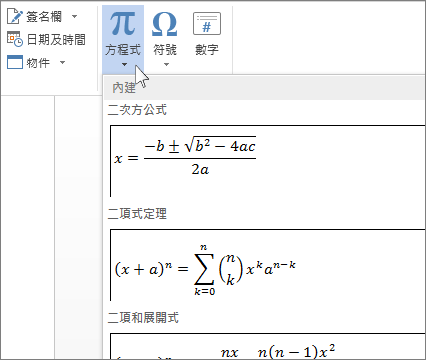
撰寫方程式或公式 Office 支援

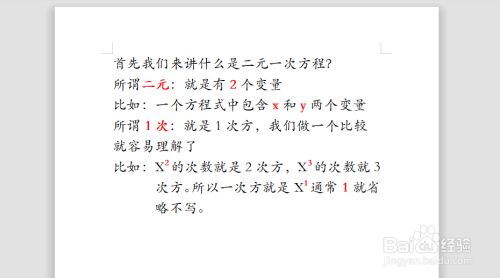
怎么解二元一次方程组 百度经验

分数的三种方法 百科全书 21

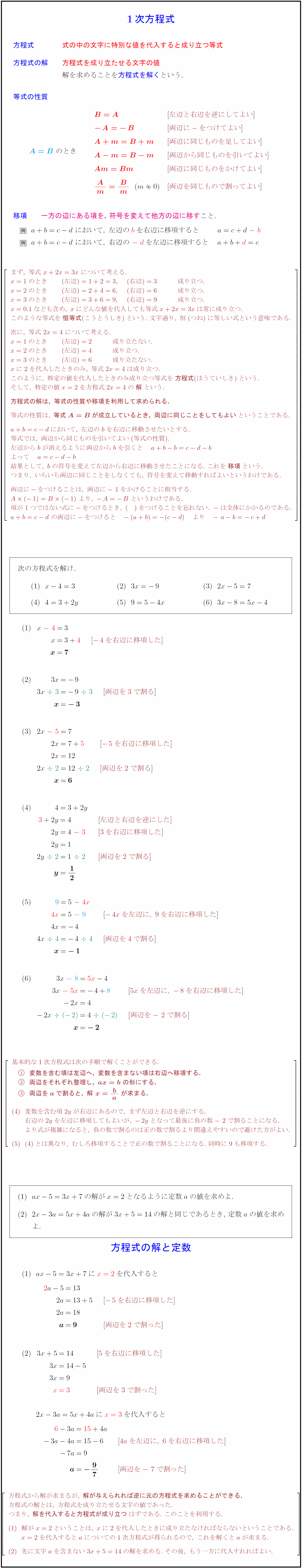
中学数学1年 基本的な1次方程式 方程式の解と定数 受験の月

中1 方程式分数 Youtube

國中數學1 3 2一元一次方程式

特斯拉 Model S 在拉力賽中挑戰一級方程式

Ch1 直線方程式 1 3 1 4 我的m讚

中学数学1年 1次方程式の利用 整数 受験の月

初二数学分式方程必备知识点和题型 方程 分式 公分母 新浪新闻

如何在长latex方程式中有换行符 How 21

初二数学分式方程必备知识点和题型

解一元二次方程式 中三 數學 Youtube

1分钟课堂丨高一化学离子方程式的含义

2

一次方程式中1

18年中考初中化学 化学方程式 知识点复习 含练习卷 每日头条

不务正业的砖工 高中化学方程式配平的代数分析 知乎

线性代数学习之线性系统 Cexo 博客园

郴州市北湖区中考化学一轮基础复习 专题九化学方程式的意义与配平下载 Word模板 爱问共享资料

中1数学 方程式とはいったいなんぞや Qikeru 学びを楽しくわかりやすく

中1 一次方程式のかっこは外してから解こう 中学数学の方程式 中間 期末テスト 高校入試対策

一元二次方程及其应用讲解 初中重点 每日头条

Incoming Term: 中 1 数学 方程式 問題,